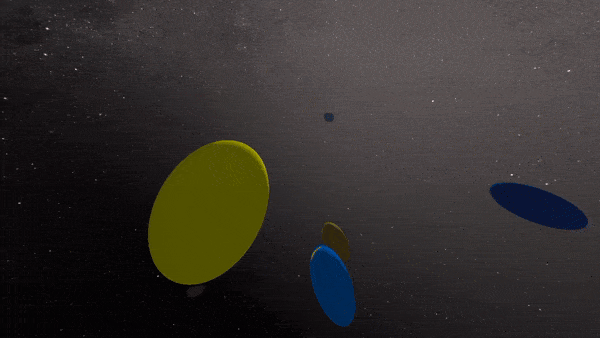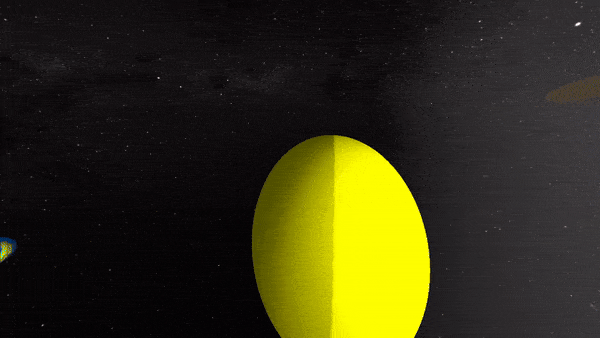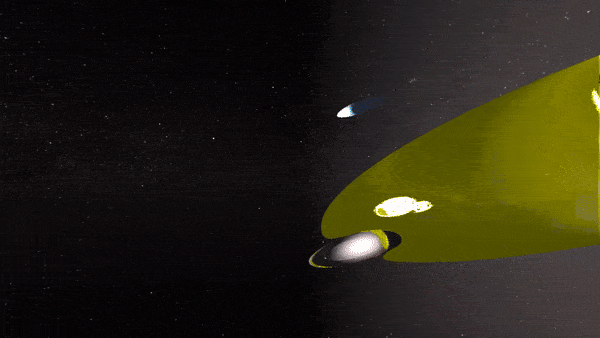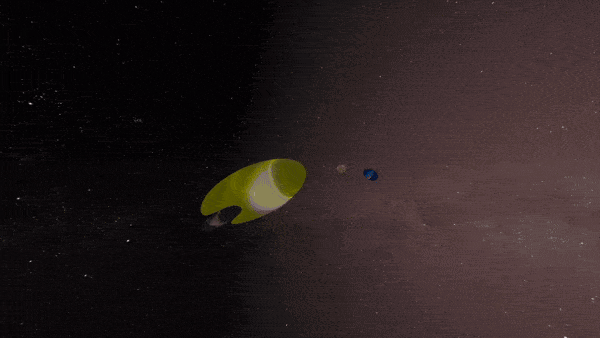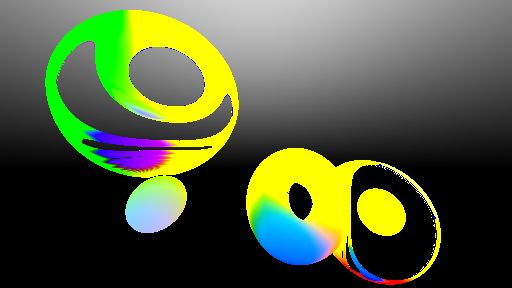GeoSim

Ray marching through hyperbolic space.

About

Title: Geo(desic) Sim(ulator)

Summary: We build a hardware accelerated ray marcher capable of rendering non-euclidian geometries in real time. In the process we developed understanding of ray marching, the mathematics of non-euclidean geometry, the CUDA programming model, and basic hardware-acceleration programming principles.

Team Members:

• Nico Castaneda
• Tianyun Yuan
• Jonathan Zakharov

Technical Approach

The project codebase revolves around CUDA. The executable is set up to run on CSUA virtual machines, with NVIDIA Tesla V100 compute. We use the nvcc compiler to generate binrary, and CMake to manage dependencies.

Libraries Used

We use C++ libraries to streamline the process, including:

LodePNG - Serializing framebuffers in memory into .png files

GLM - Linear algebra and vector mathematics

SFML - Windowing and input of interactive prototype

Additionally, we used NumPy in our Python scripts to write unit test and numerically verify our mathematical computations and results.

CUDA

Compute Unified Device Architecture (CUDA) is a parallel computing interface that allows non-serial algorithms to be off-loaded onto GPUs. We found CUDA to be particularly helpful, as the non-euclidian ray-marching algorithm can be executed in parallel: pixel values do not depend on each other. Additionally, the CUDA programming model is pretty streamless to integrate with a typical C++ workflow as long as you have access t a CUDA-capable GPU. For the most part, the difficulty of integrating CUDA just lies in passing memory pointers between the host and device.

Kernel, Block and Thread

When offloading work to GPU, we initialize a CUDA kernel, which is executed by many threads in parallel. The threads are then organized into blocks, within which the threads synchronize and communicate through shared GPU memory. This model allows for massive parallelism. In our implementation, we initialize a fixed size of CUDA blocks, each block containing a fixed size of CUDA threads. Each thread is responsible for the rendering algorithm of one pixel. We index the workers threads in a two-dimensional array, where we intuitively assign pixel coordinates to each thread, and dispatch the rendering work.

Challenges

Problem Description

For the past several decades, the focus of games and animation was to be as realistic as possible. However, there has been a recent resurgence in more stylized rendering techniques. Essentially all of existing graphics literature and techniques implicitly assume that we are working in euclidean space, which is the geometry that we experience the world in. However, while the world we live in is locally euclidean, there is ample evidence that space actually warps around mass, meaning we don't live in a perfectly euclidean universe. There are actually eight non-degenerate 3-dimensional model geometries that smoothly connect manifold surfaces and are compact. In simpler terms, there are eight geometries that actually make a decent amount of sense to render and visualize. The goal of this project is to leverage all of the things we know about light transport and rendering techniques in the typical euclidean case, and see how they work in a non-euclidean setting. There has been other work in rendering non-euclidean spaces, but these were all for the purpose of mathematical exlporations. Our goal for this project is to render hyperbolic scenes using advanced ray-marching techniques to achieve high accuracy visualizations. This work could be leveraged to create an entirely new type of visual experience that has only been minimally explored in a couple of games or short demos.

Compute

As a team of three, none of us had access to a CUDA-ready GPU. We obtained compute from CSUA that has NVIDIA GPUs. We also had a difficult time learning about the C++ compilation tooling on the remote machine. The remote machine has nvcc cuda compiler ready, however, setting up the compilation pipeline using CMake posed the team another challenge. Eventually, we managed to compile a simple cuda program. Directly writing code in cuda on a remote machine does not provide a "visual" feedback. Instead, we decide to prototype our H3 raymarching algorithm in an existing CPU-based custom pathtracer written by Jonathan.

Mathematics of Non-Euclidean Geometry

One of the greatest challenges was understanding the underlying mathematics of non euclidean geometry. We began with no exposure to any formal mathematical ideas about noneuclidean geometry. Few people have made 3D visualizations of hyperbolic space and fewer have made accessible resources. We based much of our efforts off the works of Rémi Coulon, Elisabetta A. Matsumoto, Henry Segerman, Steve J. Trettel: Ray-marching Thurston geometries and Non-euclidean virtual reality I: explorations of H3. The former being a mathematically rich but dense 140+ page dissertation on how to visualize all 8 of the Thurston Geometries. The dissertation goes into much mathematical rigor, touching on primarily geometric topology and differential geometry as well as numerical analysis and differential equations. Concepts quite foreign to us took a while to understand and implement correctly. Not having an intuition for the visuals of non euclidean geometry, many unit tests were made to verify the numerical results of all our calculations. Eventually it was all mostly understood: the different models of H3, their numerical representations, numerical stabilities, computational costs, and other pros and cons; we chose the use the hyperboloid model so we needed to know how to represent and verify that a point lie on the hyperboloid, tell if a direction was in the tangent space of a point, how to flow along the geodesics of hyperbolic space, how to represent a scene in hyperbolic space. Understanding these mathematics was crucial to creating and implementing a hyperbolic ray marcher.

Hyperbolic Raymarching

Conquering the foreign abstract mathematics and then its discrete numerical representation, we needed to adapt our home made euclidean path tracer into an interactive hyperbolic raymarcher. We first began by engineering the euclidean path tracer into a euclidean ray marcher. In a few short hundred lines of code, we succeeded. The next step was to abstract and generalize the capabilities of the ray marcher to be able to march in arbitrary geometries. Through hundreds of lines of debugging tests, hundreds of lines of dedicated scripts to sanity check numerical results, rereads of the math papers, and banging our heads against the wall, we came to a result which we know to be correct. A challenge with the alienness of non-euclidean geometry is our inability to visualize it. Days were spent realizing the fact that we could not go off visual intuition very much to verify results, hence the need to write many many numerical tests.

Solution

The Math

There are many different ways to model hyperbolic space in a way that is presentable. For the purpose of this project, we chose to utilize the hyperboloid model, which is a projective model of hyperbolic space. The following is the two-dimensional example, which generalizes up to higher dimensions:

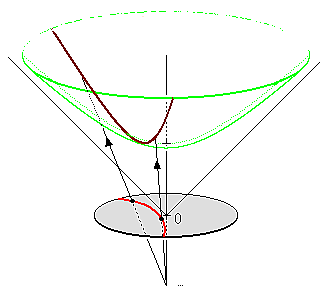
In this two-dimensional example, our hyperbolic flatlander walks along the surface of the hyperboloid, following its natural curvature. In order to visualize this flatlander in our own euclidean space, we project its hyperbolic coordinate down onto a disk that is centered below the origin. This is a very powerful and simply model of the space, as it allows us to efficiently embed the hyperbolic space in a familiar euclidean setting with very minimal overhead in terms of scene representation. However, this introduces an additional dimension, so our hyperbolic math ends up being four dimensional, which we project down to a three dimensional grid in order to render.

The Idea

With a conceptual model of hyperbolic space, the key insight that allows us to render hyperbolic scenes is simple. Assuming familiarity with raytracing, in which scenes are represented explicitly and ray-geometry intersections can be solved for analytically, ray marching is the implicit and approximate counterpart. Instead of solving an equation to find the intersection of a ray and a primitive like in raytracing, ray marching represents its primitive with signed distance functions (SDFs) which measure the signed distance between a point and the surface of the primitive. By taking the signed distance between our primitive and our ray origin, we can measure how much closer we can move or "march/step" in the direction of the ray before intersecting. We can repeat this routine until one of two conditions is met: we've reached an arbitrarily close distance from our primitive and can approximate the ray's intersection with it, or we have taken an arbitrary number of steps without reaching the previous condition, thus not intersecting any primitive. This is the algorithm of ray marching, abstract and agnostic of any geometries.

In our classical renderers and day to day lives, we assume the geometric optics model of light which states that light travels along the shortest path: along rays or straight lines. This assumption enables much of raytracing. However, dropping Euclid's fifth postulate:

"if a straight line falling on two straight lines make the interior angles on the same side less than two right angles, the two straight lines, if produced indefinitely, meet on that side on which are the angles less than the two right angles."

We leave the land of euclidean geometry, and can no longer make this assumption. In non-euclidean geometries, the shortest path between two points need not be a straight line. Yet light still does travel along geodesics. This is where we must turn to ray marching as our technique for its ability to march along the geodesic path of light. That is, we use ray marching as described above to march along the geodesic path of light in our non-euclidean space.

The Implementation

Equipped with this general method of marching rays, we now have to delve a bit into the nuances of working in hyperbolic space. Similar to moving along the surface of any non-flat object, to move along a geodesic, you move in a straight line plus some amount of curvature required to stay on the surface. In hyperbolic space, you have constant negative gaussian curvature at all points. This means each point has a local tangent space of valid directions that you can flow into. Thus, at every marching step, you not only have to flow along a curve, but you have to calculate what the new direction you are going in relative to your current position. However, due to this fundamental change in how space is laid out, many of the traditional spatial partitioning schemes used in acceleration structures like KD-trees or octrees don't work, since up is different relative to each point. Thus, for this project, we limit ourselves to the following fairly basic marching algorithm that we accelerate using CUDA:

ComputeClosestIntersection(Ray r, Scene s)
{
    Integer MAX_NUM_STEPS = X
    Scalar MIN_HIT_DISTANCE = EPS
                
    Position p = r.origin
    Direction d = r.direction
                
    for i in (1, ... , MAX_NUM_STEPS)
    {
        Scalar distance = SDF(p, scene)
                
        // Approximate Intersection
        if (distance < MIN_HIT_DISTANCE)
            return ClosestPrimitive(p, scene)
                
        // Step
        p = geodesicFlowPosition(p, d, distance)
        d = geodesicFlowDirection(p, d, distance)
    }
                
    // Ray Miss
    return NIL
}
            

In order to convert this algorithm into a GPU-friendly one, we have to first configure what is executed on the host versus what we offload onto the device, as well as ensure we have minimal communication needed between the two. In our implementation, we allocate all of the device memory on the host, load the textures, and then create a render_pixel kernel call for each pixel in the output image, which in our case is 1280x720p. After which, because we are doing fairly simple marching, we end up minimal branches throughout, and even less divergence. This allows us to effectively utilize as many of the threads at once as possible and avoid inactive threads due to branch divergence.

In addition to simply converting the CPU hyperbolic path tracer into a GPU accelerated one, we were also to add several features that greatly improve the quality of rendered images. Specifically, texture mapping, environment lighting, and environment mapping were added. This allowed us to have much more interesting renders that really showcase the fun and quirky weirdness that you are able to get from using a non-euclidean geometry.

Achievements

After pouring through math literature, we were able to successfully create a feature rich hyperbolic renderer that is able to run in real time. Specifically, at 6 rays per pixel and 6 bounces per ray, we are able to generate path traced hyperbolic scenes at 720p at around 30FPS using an RTX 3070. The following images are the results of different versions of our hyperbolic renderer.

Footage from our interactive demo of our CPU hyperbolic raymarcher prototype:

Physically-based, real-time rendering of non-euclidean sphere field:

Physically-based, real-time rendering of non-euclidean solar system:

Lessons Learned

Collaboration

Collaboration, consultation, and communication is the key to getting things done. Working in a team with some skills in common but many more disjoint proved that as a whole, you’re only as strong as the weakest link of the chain when it comes to communication. It was necessary for us to be as accommodating and empathetic as possible where we didnt excel. Furthermore, having none of us on the team be experts at mathematics let alone non-euclidean geometry, the importance of collaboration was shown to us as mathematical consultation was necessitated. We thank those at the Berkeley Mathematics Undergraduate Student Association for helping our understanding of hyperbolic geometry in this project.

Mathematics

Mathematical understanding, and more broadly, all understanding cannot be rushed. One can reasonably estimate the times it takes to perform a feat of physical labor. One can also, with less accuracy though, estimate the times it takes to perform a feat of engineering. However one cannot accurately estimate the times it takes to perform a feat of intellectuality. Intellectual deadlines need to be taken with a grain of salt because it is difficult to know when a concept will make sense. Yet in a context such as industry, academia, or this project, where deadlines are final, it only means they need to be treated with a lot more respect and caution. One cannot foresee when a concept will make sense, thus they must be proactive as resources permit.

Contributions

Nico Castaneda: Compute, CUDA ray marcher, and general optimizations

Tianyun Yuan: Compute, CUDA ray marcher, DevOps, texture mapping, environment mapping, environment light, and scene architecture

Jonathan Zakharov (me!): Mathematics, hyperbolic ray marching prototype (C++ & SFML), numerical testing

Personal Contributions

In the GeoSim project, I took on a crucial role, focusing on the mathematical aspects and the development of the hyperbolic prototype. My journey began with a deep dive into the mathematical theories essential for implementing non-Euclidean geometry. This involved grappling with intricate concepts such as the hyperboloid model, hyperbolic space, and geodesics—key elements for hyperbolic ray marching.

With no prior knowledge of the mathematics of non euclidean literature, I dove head first into books and research papers to build a solid foundation of these complex topics. My objective was to translate these theoretical concepts into practical algorithms for rendering hyperbolic space. This process included adapting our existing Euclidean path tracer to function within a non-Euclidean framework.

My greatest contribution was the development of a hyperbolic ray marcher prototype. This task demanded precise coding and rigorous testing to ensure that the new system could accurately simulate hyperbolic geometry. I meticulously verified that the mathematical computations were correct both numerically and visually. I faced numerous challenges, such as ensuring the precision of ray intersections and optimizing performance for real-time rendering.

Extras

Bug art

Additional Links

• Development Video
• Demo Video
• Presentation