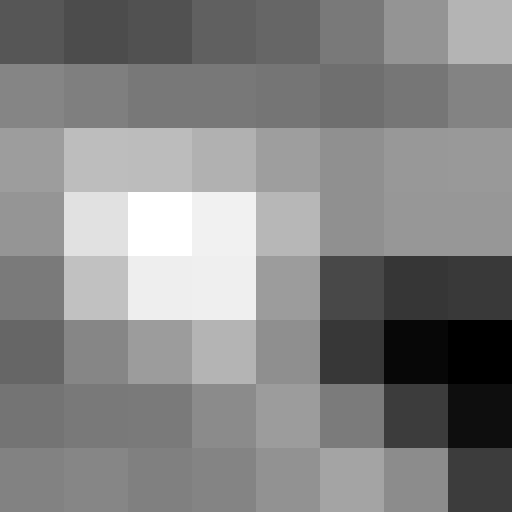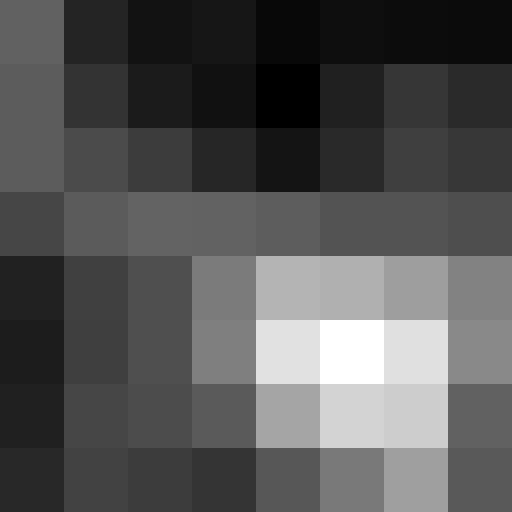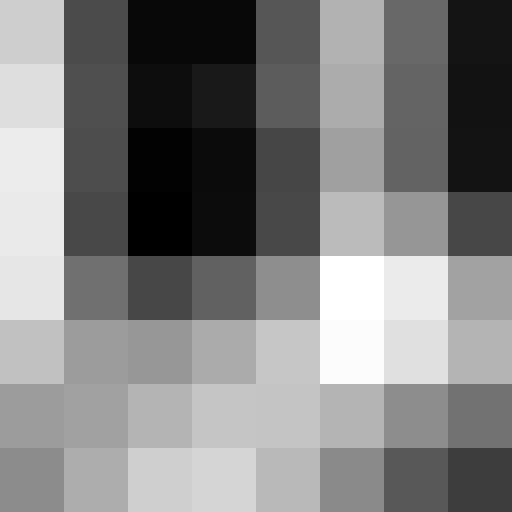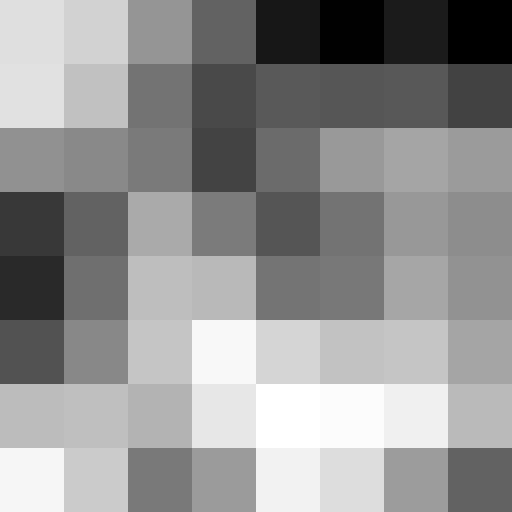Image Panoramas

By Jonathan Zakharov

Introduction

This project focused on implementing perspective image warping and mosaicing to create panoramic images from multiple images. This was accomplished by computing the homographies between images, warping said images, and then blending them together into panoramas. Through this project, we gained practical experience with concepts in linear algebra, computational photography and computer vision, learning how to make our own panoramic images from scratch.

Starting Images

Implementation

To begin, we needed to go out and take photos such that we could compute the homographies between images in a set. A perspective transform or a homography relates two images when they have a shared center of projection. In practice this means taking photos of a scene from the same exact position, only changing the pitch and yaw along the axis of rotations of the camera.

Here we capture some photos of Cal, the bay, and the cluttered desk I sit at now.

Recovering Homographies

Mathematical Foundation

A homography is a projective transformation that maps points from one plane to another. In the context of image processing, it allows us to relate two images of the same planar surface taken from different viewpoints. Mathematically, a homography $H$ is represented by a 3x3 matrix:

$$ H = \begin{bmatrix} h_{11} & h_{12} & h_{13} \\ h_{21} & h_{22} & h_{23} \\ h_{31} & h_{32} & h_{33} \end{bmatrix} $$

This matrix has 9 elements, but because it is defined up to a scale factor, it effectively has 8 degrees of freedom. Given a point $(x, y)$ in the first image and its corresponding point $(x', y')$ in the second image, the homography relation can be expressed as:

$$ \begin{bmatrix} wx' \\ wy' \\ w \end{bmatrix} = H \begin{bmatrix} x \\ y \\ 1 \end{bmatrix} $$

$$x' = \frac{h_{11}x + h_{12}y + h_{13}}{h_{31}x + h_{32}y + h_{33}}$$ $$y' = \frac{h_{21}x + h_{22}y + h_{23}}{h_{31}x + h_{32}y + h_{33}}$$

Linear System Setup

To solve for the homography matrix, we rearrange these equations into a linear system. For each point correspondence, we get two equations:

$$x'(h_{31}x + h_{32}y + h_{33}) = h_{11}x + h_{12}y + h_{13}$$ $$y'(h_{31}x + h_{32}y + h_{33}) = h_{21}x + h_{22}y + h_{23}$$

These can be rewritten as:

$$ \begin{bmatrix} x & y & 1 & 0 & 0 & 0 & -xx' & -yx' & -x' \\ 0 & 0 & 0 & x & y & 1 & -xy' & -yy' & -y' \end{bmatrix} \begin{bmatrix} h_{11} \\ h_{12} \\ h_{13} \\ h_{21} \\ h_{22} \\ h_{23} \\ h_{31} \\ h_{32} \\ h_{33} \end{bmatrix} = \begin{bmatrix} 0 \\ 0 \end{bmatrix} $$

Implementation

The compute_homography function in warp_img.py implements this process by setting up the system of linear equations $Ah = 0$, where $A$ is the matrix of coefficients from the equations above, and $h$ is the vector of homography matrix elements.

With 4 point correspondences, we get 8 equations, which is sufficient to solve for the 8 degrees of freedom in the homography matrix. However, to improve robustness, we typically use more than 4 points and solve the overdetermined system using the least squares method. This is just a call to np.linalg.lstsq.

Results

We illustrate the effect of a perspective transform on a grid. The right image was create with the help of Photoshop's perspective warp tool. Applying the homography to the grid indeed gives us the same perspective transformed grid.

Image Warping

Implementation

Once the homography is computed, we want to warp one image to align with another in the same image plane. The warp_image function in warp_img.py implements inverse warping for this purpose. It computes the inverse of the homography matrix and, for each pixel in the output image, calculates the corresponding location in the input image. To ensure all warped content is captured in the output image, we implement a helper method compute_warped_image_bb which calculates the bounding box and displacement of the warped image by transforming the corners of the original image.

Results

Image Rectification

Implementation

Image rectification serves as a benchmark for the success of our homography calculations and image warping implementations. Our rectify_image function in rectify.py demonstrates this process by taking an input image, a set of points defining a rectangular object in the image, and the desired dimensions of the rectified object. It computes a homography between these points and a predefined rectangular grid, then applies this homography to warp the entire image. This process effectively simulates rotating the camera to point directly at the planar surface, removing perspective distortion. Successful rectification results in an image where the selected object appears as a rectangle, verifying that our homography and warping functions work.

Results

Blending and Mosaic Creation

Implementation

The ultimate goal of this project is to create panoramic images. With our successful implementation of image warping, the final step is to blend our warped images. The blend_images function in mosaic.py implements a simple blending technique. It creates a panorama canvas large enough to accommodate both images, places the second (unwarped) image onto the canvas, and then computes an average of the two images in the overlapping region.

The main function in mosaic.py outlines the overall mosaic creation process: first, it computes the homography between two images, then warps the first image to align with the second, and finally blends the warped image with the second image. While this approach produces a basic mosaic, it can result in some seams or ghosting artifacts when there are significant differences between images, like in lighting/exposure.

Results

Panorama Automation

Introduction

In the previous part of the project, we successfully automated the process of creating panoramic photos, given a set of images from the same center of projection with explicit specification of feature points in images and their correspondences between images. Our goal now is to create panoramic images without the need to explicitly specify points and their correspondences between images. In other words, we want to develop a system for automating the detection, matching, and transformation of key image features in images. Our procedure will look like this

• Detecting features in images.
• Extracting descriptors for detected features.
• Matching descriptors between images.
• Computing homographies with RANSAC.
• Mosaicing images into a panorama.

The result is to fully automatically generate panorama photos given only the images to mosaic as input.

Feature Detection

Implementation

Our goal in automatic image mosaicing is to automate the process of manually selecting correspondences between sets of images. To begin, we need to find feature points in an image that will have correspondences in other images we plan to mosaic together. Harris corner detection is a simple and effective way of identifying many high-interest regions or “corners” in each image that are likely to have corresponding points in other images.

The Harris Corner Detector is well-suited for detecting corner features that remain consistent across images. Due to its robustness, it was chosen to automate the task of identifying points that would otherwise need to be manually selected as correspondences for image stitching. We used an existing implementation of Harris corner detection, which returns all detected corner points, giving us thousands of feature points on each image. The next step is to determine which features in one image have corresponding features in another.

Results

Feaure Description Extraction

Implementation

Now that we have a good set of candidate points throughout our images, we need a way to identify which features in one image correspond to features in another. We achieve this by performing feature descriptor extraction. For each detected feature, a feature descriptor is extracted from a 40x40 pixel patch centered on the feature. To make patches robust to noise and minor lighting changes, bias/gain normalization and Gaussian blur were applied, and patches were resized to an 8x8 array, reducing computational complexity without sacrificing uniqueness.

Results

Here are some 8x8 image patches extracted after extraction from Harris Corner Detection, lowpassed, normalized, and downscaled.

Feature Matching

Implementation

With two images and their sets of image feature patches, we aim to determine which features in one image have matching features in another. This is achieved using a K-D Tree with the 2-Nearest Neighbors (2-NN) approach. Lowe’s ratio test was applied to ensure that matches are reliable by comparing the two nearest neighbors of each point and retaining only those with clear closest matches.

We now have automatically generated matching points between images, identifying which points on multiple images correspond to each other. We’ve successfully automated the task of selecting matching points between images. Or have we?

Results

Here are some image feature correspondence pairs. Notice how the correspondnces aren't perfect to create some invariance to transformations.

Here we visualize the strongest correspondence found between the images at the base of The Campanile.

Here are all of the correspondences between images, annotated by points of the same color. Notice the presence of false positive correspondences, but a majority cluster of true positives.

Homography Computation Using RANSAC

Implementation

Feature matching performs well but may produce some false positives, resulting in outlier correspondences that reduce the accuracy of our least squares estimation when computing homographies between images. Our final step is to compute the homography using RANSAC, aligning matching points between images while detecting and removing outlier correspondences. This was achieved by iteratively selecting four random points to compute candidate homographies and evaluating the inliers based on a distance threshold. Of these candidate homographies, the one with the most inliers is used to compute the final homography using standard least squares.

Results

We compare the results of our RANSAC-based homography estimation to the manual homography estimation. The differences are minimal, indicating that our RANSAC-based estimation is robust to outliers and produces a homography that is consistent with the manual estimation.

Putting it all Together

Taking our algorithms for automatically computing homographies, we then warp and blend the images together as before, achieveing fully automated panorama creation. The results of this process are shown below and nearly indistinguishable from the manual process. Success!

Conclusion

Among the coolest things I've taken away from is RANSAC. Having not known about RANSAC before, I fint it is a fascinatingly robust and versatile statistical tool. I could see myself using it for many things. It was also really rewarding to be able to automate something which was laborious and not a straight forward/obvious computation.

This project provided valuable hands-on experience with fundamental techniques in computational photography and computer vision. By implementing homography computation, image warping, basic blending, image feature detection, and image feature matching, we gained practical insight into the challenges and intricacies of creating panoramic images from multiple photographs.